A Language Speed Test Comparing Embedded Linux Boards

I recently ran across Yet Another Language Speed Test: Counting Primes (C, C++, Java, JavaScript, PHP, Python and Ruby).

This is a fairly interesting test because of its simplicity when implementing across many different programming languages- even if it is not tailored specifically to idioms and abstractions provided by those languages. The test referenced above directly compares programming language speeds and this one instead compares those programming language speeds on different embedded Linux boards. This is not a test to optimize the languages, the code, or the boards to be as fast as possible. Instead it is intended to run the same exact code using the same runtime version of a language on different embedded Linux boards in as identical an environment as possible.

The test code is very simple. When given a number n, the program simply counts the number of prime numbers found up to and including n. The test code is implemented in the following languages:

• C (gcc using -O2 optimization)
• Python 2.7.10 (using -O optimization)
• Python 2.7.10 (Compiled) (using -O optimization)
• Ruby 2.2.2p95
• Lua 5.1.5
• PHP 5.6.12
• Javascript (nodejs v0.10.40)

on the following boards:

• MIPS Creator CI20
• Raspberry Pi 2
• Raspberry Pi Model B
• BeagleBone Black

The final result is enlightening. Here is the comparison of counting prime numbers up to 2²⁴. The runtimes here are significant enough to get a good comparison across boards in each of the languages tested. Note that lower times mean faster.

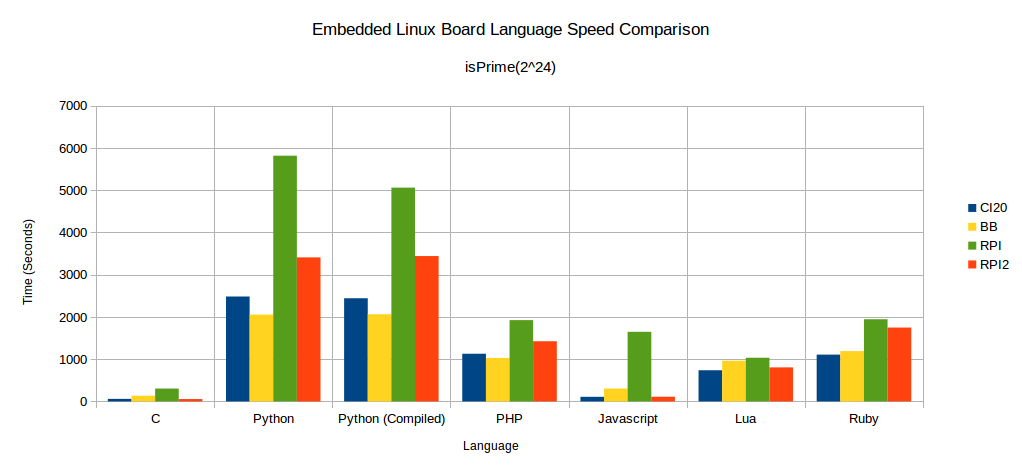
If a lower value of n is charted, where n is 2¹², this puts far more weight on startup and initialization times of the test programs.

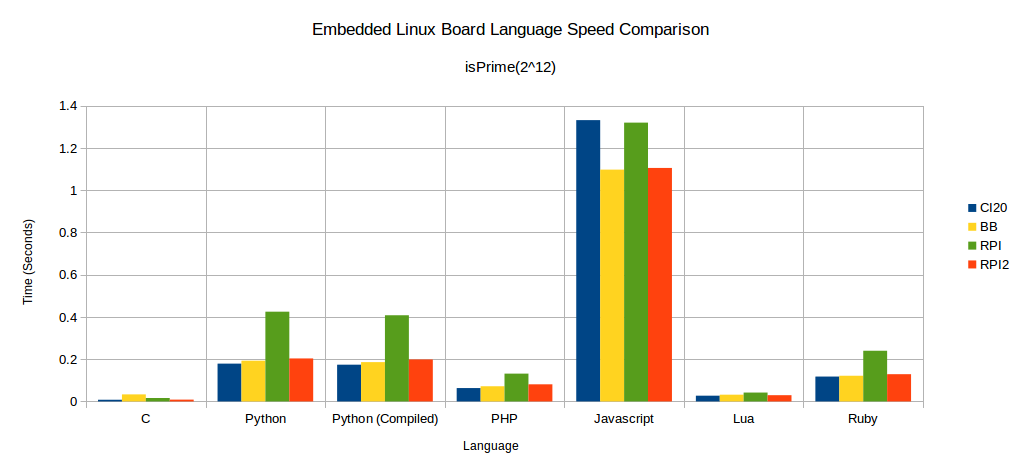
Below are charts of the raw and complete data for each of the boards. The full tests are run with n being from 2¹² to 2²⁴.

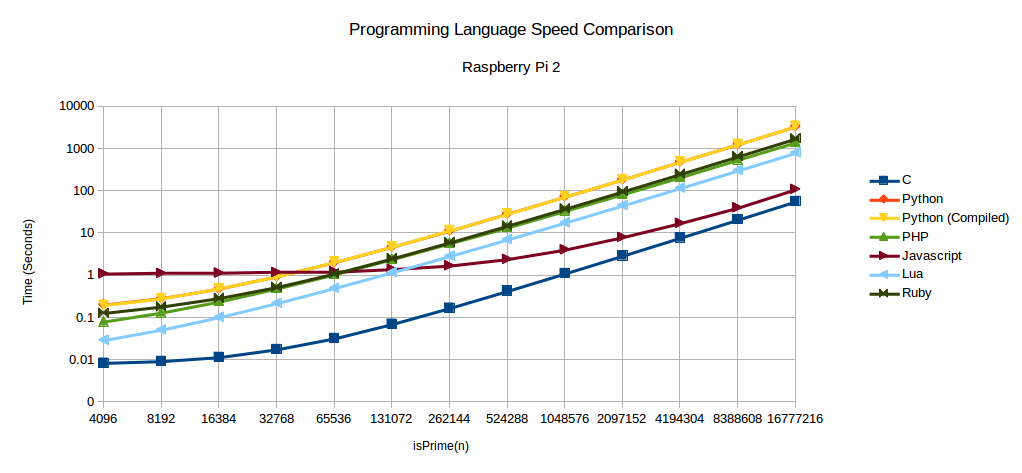
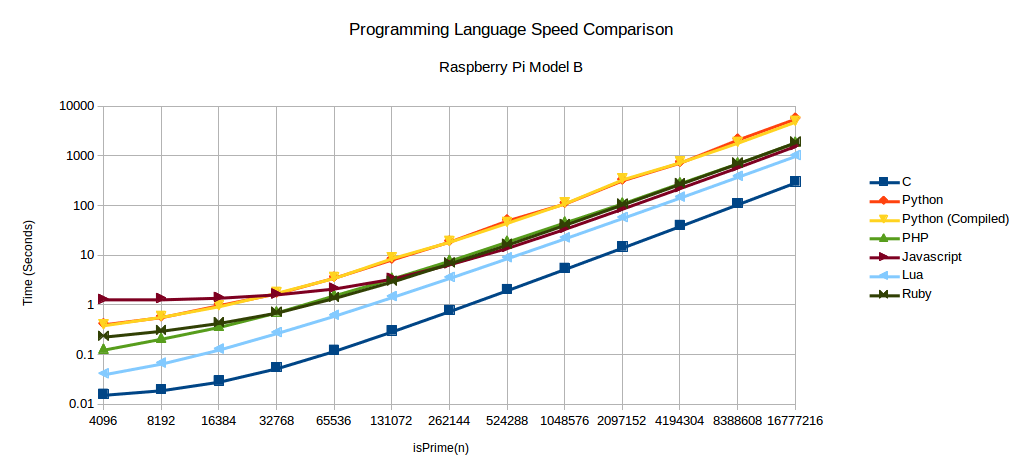
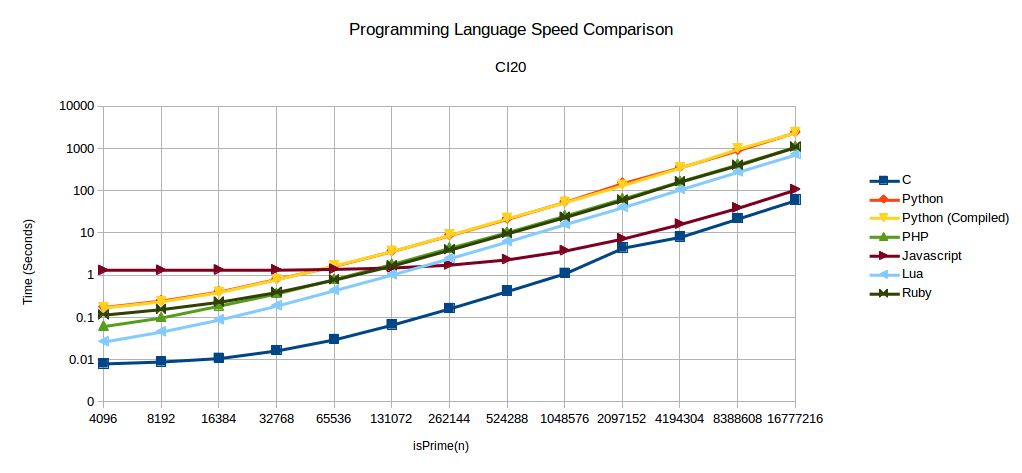
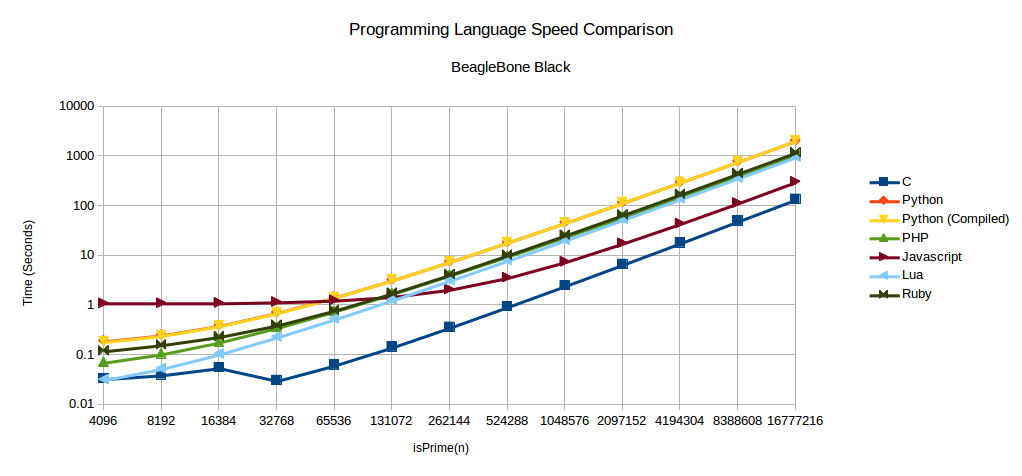
Do you see that drop in there in the BeagleBone Black C language data? All data was collected twice and that abnormality existed in both of them. I went back and manually ran the test and the same thing happened. Just wanted to point out this is not a mistake and I am wondering what happens there.

This basic test is enough to heat up every single processor enough to be fairly warm to the touch. The BeagleBone black got the hottest with a 142F reading on the surface of the SoC.

The test consisted of building the same version of buildroot default configurations for all boards. This included creating bootloaders, a kernel, and a rootfs containing the languages and test code on a uSD/SD card. These were all setup in a headless configuration with the only interface being a serial console. It turns out, this was quite a time consuming processing to get setup for each board.

CI20

BeagleBone Black

Raspberry Pi 2

Raspberry Pi Model B

The following are the actual test programs written in the various languages to compute the number of prime numbers given an argument of n.

Lua

function isPrime(n)
   if (n < 2) then
      return false
   elseif (n == 2) then
      return true
   elseif (n % 2 == 0) then
      return false
   end
 
   for i = 3, math.sqrt(n), 2 do
      if (n % i == 0) then
         return false
      end
   end
 
   return true
end
 
local noPrimes = 0
local limit = tonumber(arg[1])
for n = 0, limit, 1 do
   if isPrime(n) then
      noPrimes = noPrimes + 1 
   end
end
 
print(string.format("pi(%d)",noPrimes))

C

#include <stdio.h>
#include <math.h>
#include <stdlib.h>
 
int isPrime(int n) {
   if (n < 2)
      return 0;
   else if (n == 2)
      return 1;
   else if (n % 2 == 0)
      return 0;
 
   int upperLimit = sqrt(n);
   int i = 3;
   while (i <= upperLimit) {
      if (n % i == 0)
	 return 0;
      i += 2;
   }
   return 1;
}
 
int main(int argc, char** argv) {
  int noPrimes = 0;
  int limit = atoi(argv[1]);
   for (int n = 0; n <= limit; n++) {
      if (isPrime(n))
	 noPrimes ++;
   }
   printf("pi(%d)\n", noPrimes);
   return 0;
}

Javascript

function isPrime(n) {
    if (n < 2)
        return false;
    else if (n == 2)
        return true;
    else if (n % 2 == 0)
        return false;
    var uL = Math.sqrt(n) | 0, i = 3;
    while (i <= uL) {
        if (n % i == 0)
            return false;
        i += 2;
    }
    return true;
}
 
var noPrimes = 0;
var limit = process.argv[2];
 
for (var i = 0; i <= limit; i++) {
    if (isPrime(i))
        noPrimes++;
}
 
console.log("pi(" + noPrimes + ")");

PHP

<?php
function isPrime($n) {
   if ($n < 2)
      return false;
   elseif ($n == 2)
      return true;
   elseif ($n % 2 == 0)
      return false;
   $ul = sqrt($n);
   $i = 3;
   while ($i <= $ul) {
      if ($n % $i == 0)
	 return false;
      $i+=2;
   }
   return true;
}
 
$noPrimes = $i = 0;
$limit = $argv[1];
 
while ($i <= $limit) {
   if (isPrime($i))
      $noPrimes++;
   $i++;
}
 
printf("pi(%d)\n", $noPrimes);
?>

Python

from math import sqrt
import sys
 
def isPrime(n):
    if (n < 2): return False
    elif (n == 2): return True
    elif (n % 2 == 0): return False
 
    upper_limit = int(sqrt(n))
    i = 3
    while (i <= upper_limit):
        if (n % i == 0): return False
        i += 2
 
    return True
 
lim = int(sys.argv[1])
no_primes = 0
n = 0
 
while (n <= lim):
    if (isPrime(n)): no_primes += 1
    n += 1
 
print ("pi(%d)" % (no_primes))

Ruby

def isPrime n
    return false if n < 2
    return true if n == 2
    return false if n % 2 == 0
 
    upper_lim = (Math.sqrt n.to_f).to_i
    i = 3
    while i<= upper_lim
        return false if n % i == 0
        i+=2
    end
 
    true     
end
 
lim=(ARGV[0]).to_i
no_primes = 0
 
i = 0
while i <= lim
  no_primes += 1 if isPrime i
  i+=1
end
puts "pi(#{no_primes})"